Stima dimensionamento linee IVR

• 29/12/2022
• Tempo di lettura: 4 minuti.

Stimare il numero delle chiamate in ingresso ad un sistema IVR e di Call Center, così come effettuare una stima della distribuzione delle chiamate nel tempo, è di fondamentale importanza per dimensionare opportunamente il sistema in termini di risorse da impiegare. In particolare, per effettuare un dimensionamento che sia poi realistico è necessario stimare il numero massimo di chiamate contemporanee in arrivo al sistema.

L’andamento secondo cui si distribuiscono le chiamate in ingresso ad un sistema di Call Center durante le ore del giorno è una questione ampiamente studiata in letteratura, e tali studi possono essere sfruttati per tentare di stimare l’impegno massimo del sistema a partire da dati di traffico giornalieri per esempio. La figura che segue mostra la distribuzione oraria tipica delle chiamate in ingresso ad un sistema di Call Center ¹.

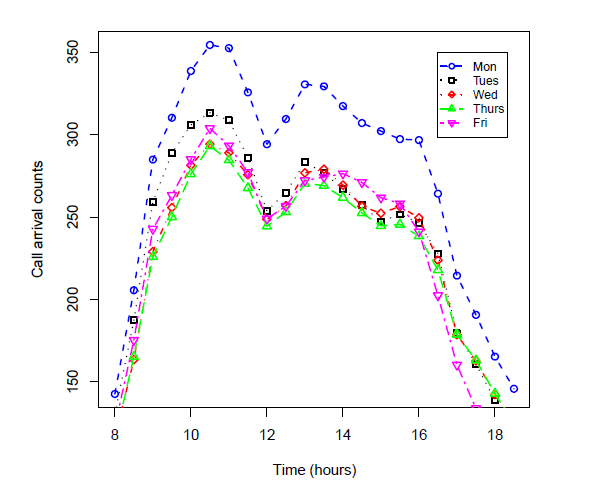
Non sempre si hanno a disposizione dati di traffico con granularità oraria delle chiamate, mentre dati giornalieri sono molto più comuni. Partendo però da un determinato range di giorni, anche limitato, in cui si hanno disponibili dati di traffico orari, sarà possibile andare a calcolare “pesi” orari che rappresentano la percentuale di chiamate giornaliere arrivate in una determinata fascia oraria, da applicare poi a dati giornalieri, in modo da ottenere il picco orario con cui poter stimare l’impegno massimo del sistema, in termini di massimo numero di chiamate contemporanee attive. Come già detto prima, è bene ripetere il concetto che si tratta di stime, oltretutto legate alla particolare tipologia di servizio e di sistema, pertanto sarà necessario tenere conto di opportuni sovradimensionamenti a salvaguardia di quello che poi potrà essere il traffico reale.

Supponiamo quindi di avere a disposizione dati di traffico orari per 4 giorni su un determinato servizio IVR, attivo in un certo periodo del giorno, e calcoliamo le percentuali con cui le chiamate si distribuiscono sulle singole fasce orarie, per poi andare a calcolare i valori medi di tale percentuali. Il calcolo è effettuato semplicemente andando a dividere il numero di chiamate in ciascuna fascia oraria per il totale delle chiamate ricevute nel giorno specifico.

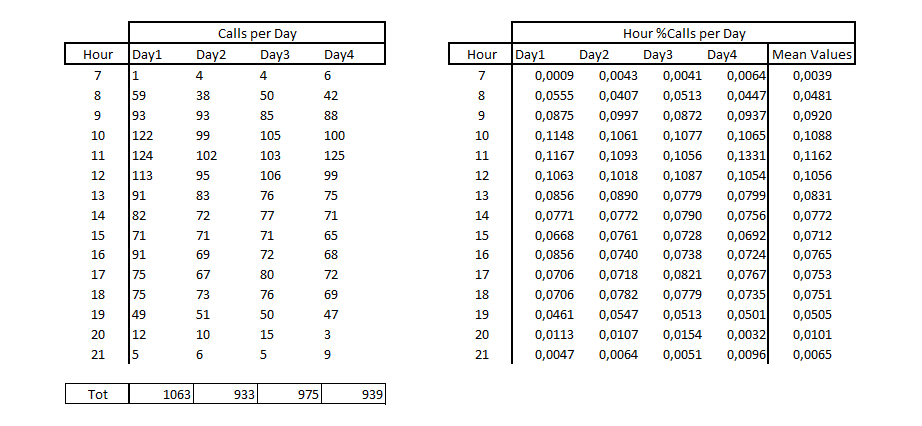
Dai grafici delle distribuzioni orarie delle chiamate, così come i valori in percentuale ottenuti, è evidente il tipico andamento giornaliero.

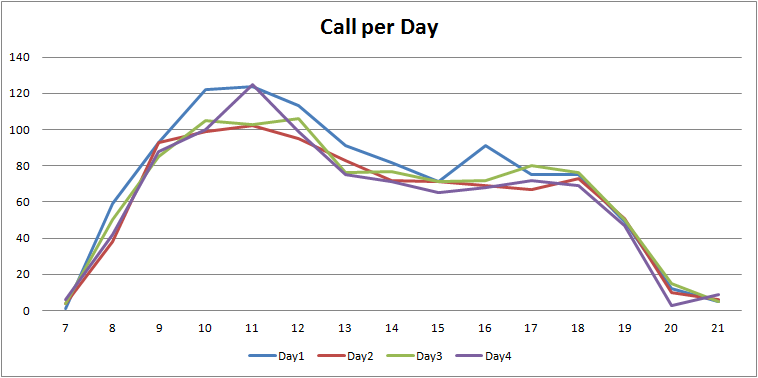
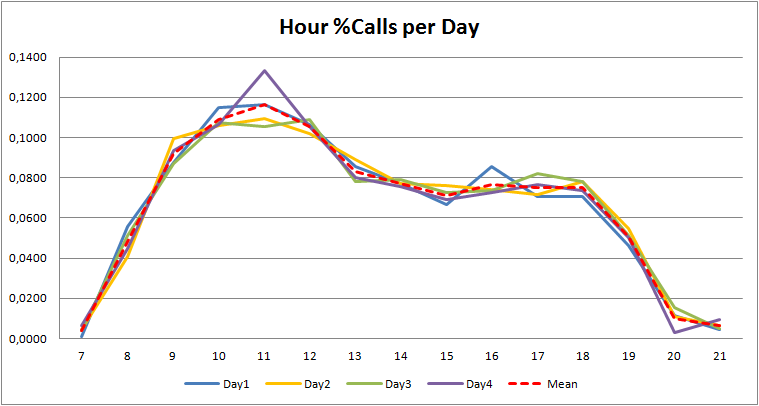
I valori medi ottenuti nel calcolo precedente, possono essere utilizzati come pesi da applicare al totale giornaliero di chiamate ricevute per poter stimare le distribuzioni orarie.

Supponendo quindi di voler stimare la distribuzione oraria per un determinato giorno, in cui sappiamo essersi verificato un picco di chiamate pari a 21700, otterremo picchi di chiamate orarie superiori alle 2000 chiamate, ed il valore di picco ottenuto può essere utilizzato come input per la distribuzione Erlang B per andare a stimare il numero massimo di chiamate contemporanee attese sul sistema.

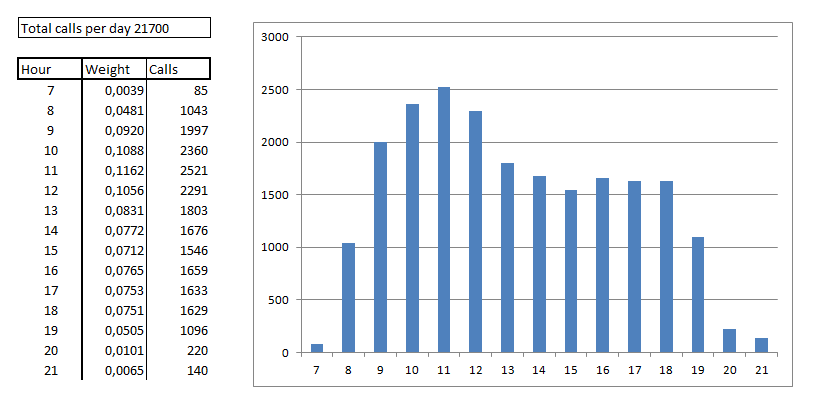
A questo punto, ottenuto il dato di picco pari a 2521 chiamate, ed approssimando la durata media delle chiamate (es. 90 secondi), sarà possibile utilizzare la formula Erlang B per stimare il numero di linee necessarie per avere un sistema con una certa probabilità di blocco.

La formula Erlang B rappresenta la probabilità di blocco in un sistema con perdita cioè senza possibilità di attesa in coda. Esprime quindi la probabilità che un utente (o più in generale una chiamata) in arrivo su un sistema con n linee e senza possibilità di accodamento venga rifiutata in quanto tutte le linee sono occupate.

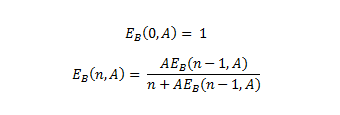
Dove:

• E è la probabilità di blocco
• n è il numero di linee
• A è il traffico espresso in Erlang (traffico effettivo/attivo in un’ora)

La formula Erlang B è resa disponibile anche come tabella Erlang-B-Table.xls, molto utile e di immediata interpretazione permette di ottenere sia il valore di E a partire da n e A, sia il valore di n a partire da E e A.

Nel nostro caso, la variabile da calcolare è proprio n, dato che abbiamo stimato A e andremo a considerare il valore di E più basso possibile.

Supponendo quindi che il numero massimo di chiamate in un’ora è 2521 con durata media 90 secondi, il valore di A è 2521 x 90 / 3600 e cioè A = 63. A questo punto utilizzando la formula Erlang B tabellare e scegliendo una probabilità di blocco pari a 0.1% risulta che con Erlang pari a 63 il sistema in questione dovrà essere dimensionato per poter ricevere 86 chiamate in contemporanea.