IVR capacity calculation, how to estimate the number of ports

• 29/12/2022
• 4-minute read

Estimating the number of incoming calls to an IVR or Contact Center system, as well as estimating the distribution of calls over time, is of fundamental importance for correctly sizing the system in terms of resources to be used. In particular, for a realistic sizing, it is necessary to estimate the maximum number of simultaneous calls arriving to the system.

The trend according to which incoming calls are distributed to a Contact Center system during the day is a subject widely studied in the literature, and these studies can be exploited to try to estimate the maximum commitment of the system, starting for example from the data of daily traffic. The following figure shows the typical hourly distribution of incoming calls to a Contact Center system ¹.

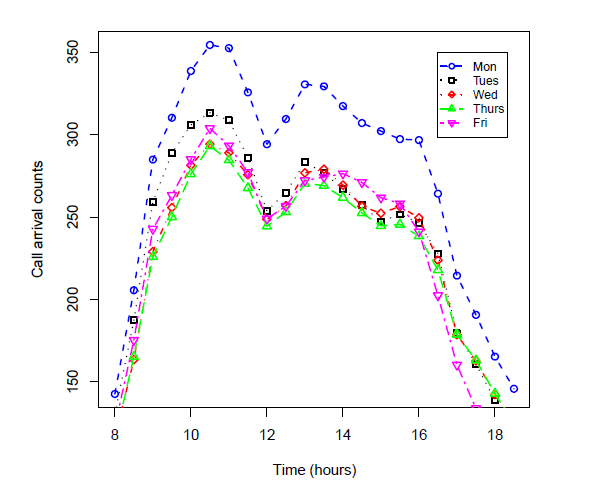
Hourly granular call traffic data is not always available, while daily data is much more common. However, starting from a specific range of days, even limited, in which hourly traffic data is available, it will be possible to calculate hourly “weights” which represent the percentage of daily calls arriving in a specific time slot. These “weights” then can be applied to daily data, in order to obtain the hourly peak beeing able to estimate the maximum load of the system, in terms of maximum number of simultaneous calls. As already mentioned before, we’re talking about estimation, that is also related to the particular type of service and system, therefore it will be necessary to take into account an appropriate oversizings to safeguard what will then be a realistic traffic distribution.

Let’s assume that we have hourly traffic data available for 4 days on a specific IVR service, active in a certain period of the day, and we calculate the percentages with which the calls are distributed over the individual time slots, and then calculate the average values of that percentage. The count is obtained by dividing the number of calls in each time slot by the total number of calls received on the specific day.

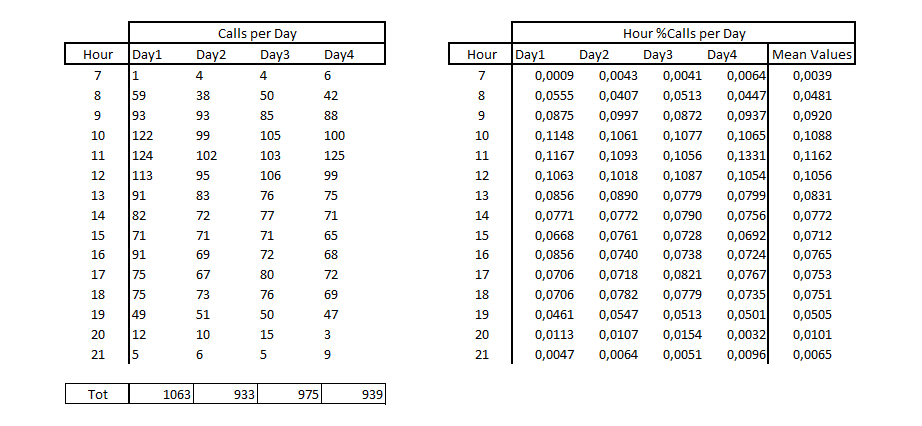
The graphs of the hourly distribution, as well as the percentage values, show the typical daily trend.

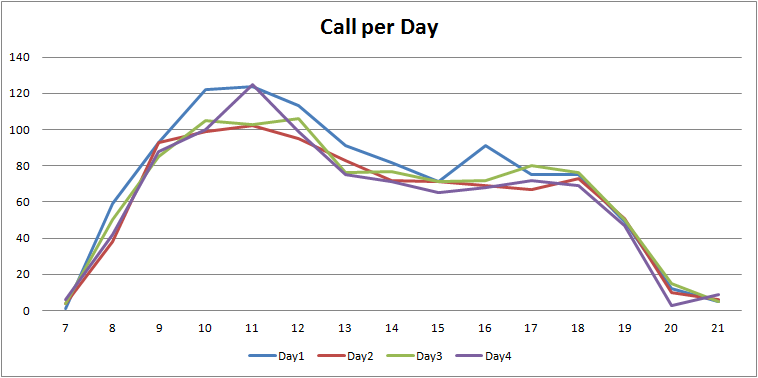
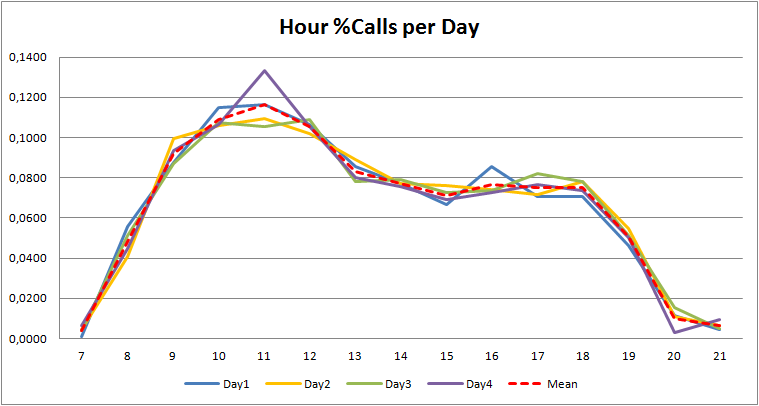
The mean values obtained in the previous calculation can be used as weights to be applied to the daily total of calls received, and estimate hourly distributions.

Supposing we want to estimate the hourly distribution of a given day, in which we know that there was a peak of calls equal to 21700, we will obtain peaks of hourly calls greater than 2000, and the peak value obtained can be used as input for the Erlang B distribution, in order to estimate the maximum number of concurrent calls expected on the system.

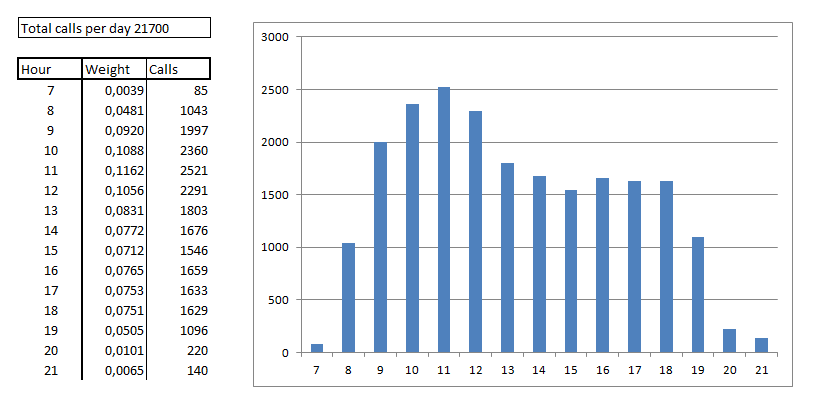
Now, having the peak of calls equal to 2521, and approximating the average duration of the calls (e.g. 90 seconds), it will be possible to use the Erlang B formula to estimate the number of ports necessary to guarantee a system with a certain probability of saturation.

The Erlang B formula represents the probability of blocking in a losing system, i.e. with no possibility of waiting in queue. It therefore represent the probability that a user (or more generally a call) arriving on a system with n lines and without the possibility of queuing will be rejected because all the lines are busy.

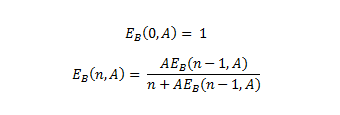
Where:

• E is the probability that a customer request will be rejected due to lack of resources
• n is the total number of ports in the system
• A is the total traffic in erlangs

The Erlang B formula is also made available as a table Erlang-B-Table.xls, very useful and of immediate interpretation, it allows to obtain both the value of E given n and A, and the value of n given E and A.

In our case, the variable to be calculated is just n, given that we have estimated A and we will consider the lowest possible value of E.

Assuming that the maximum number of calls in an hour is 2521, with an average duration of 90 seconds, the value of A is 2521 x 90 / 3600 and so A = 63. At this point using the table for Erlang B formula and choosing a probability of block equal to 0.1% it turns out that with Erlang equal to 63 the system should be able to receive 86 concurrent calls.